[Tensorflow] 08 Deep Neural Nets의 기본 학습하기
01. Deep Neural Nets
이번 포스트에서는 Deep neural nets의 기본 개념을 알아보겠습니다.
![]()
위 그림은 우리 몸 속 곳곳에 있는 신경세포를 도식화 해놓은 것입니다. Cell body의 수많은 Dendrites로부터 Input을 받고 길게 뻗어있는 꼬리인 Axon을 통해 신호를 전달합니다. Axon terminal은 그 다음 신경세포 혹은 근육 등과 연결되어 있어 이후 단계에 Output 신호를 전달합니다. 이러한 신경세포는 특히 뇌에 많이 분포되어 있겠죠. 신경세포를 Neuron(뉴런)이라고 부릅니다. 과학자들은 이런 뉴런의 구조에 착안하여 컴퓨터 학습 모델을 구현하고자 하였습니다.
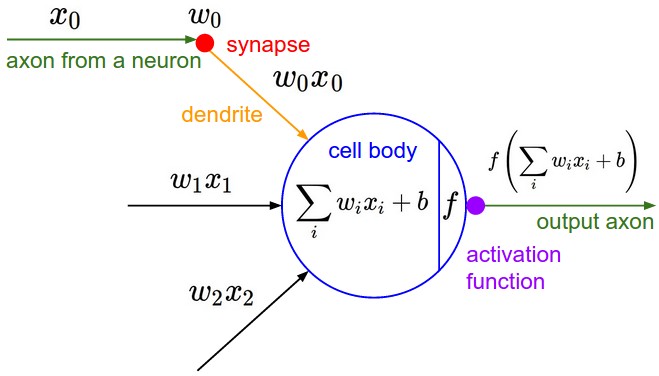
컴퓨터의 뉴런은 인체의 뉴런과 마찬가지로 Dendrite를 통해 이전 뉴런들로부터 수많은 정보( )를 받습니다. 그림에서 Synapse는 뉴런과 뉴런 사이를 의미합니다. Dendrite로 들어온 Input 정보들은 각각의 특성에 맞게 비중(
)이 달라집니다. 모든 신호가 합쳐지고 Axon을 통과하여 최종적인
처리(Activation function)가 끝나면 output 신호가 결정됩니다. Output 신호는 다시 Synapse를 거쳐 다음 뉴런으로 전달됩니다. 여태까지 우리가 봐왔던 것들과 똑같습니다. 가설을 설정하고 cost function을 만들어서 실제값과 비교하는 것과 구조가 일치합니다.
02. XOR problem
머신러닝의 발전 과정에서 한 가지 문제가 등장합니다. 바로 XOR problem이라는 것입니다.
![]()
위 그림에서 AND와 OR은 선으로 분할이 가능(Linearly separabe)한데 반하여 XOR은 그렇지 못합니다. 즉, 우리가 여태까지 해왔던 방법으로는 XOR problem을 학습시킬 수가 없다는 뜻입니다. 우리는 여태껏 직선(혹은 면)을 하나 혹은 여러 개 긋는 작업을 한 것이지 곡선을 만들거나 그런 적은 없었습니다. 직선을 하나 긋는 데에는 학습시킬 뉴런이 1개이면 충분했습니다. 다른 말로 Layer가 1개인 상태의 머신러닝을 구현해 왔던 것입니다.

해결책은 그렇다면 여러개의 Layer(Multilayer neural nets)를 구현하면 되지 않느냐는 것이었습니다, 좋은 해결책이었습니다. Input layer와 Output layer 사이에서만 이루어지던 학습을 분할하여 여러번 진행되도록 하였더니 XOR 값을 100% 정확히 예측하게 되었습니다. Layer를 여러 개 만들게 되면서 명칭 역시 “머신러닝”에서 “딥러닝”으로 옮겨가게 됩니다.
딥러닝은 모든 것을 해결해줄 것처럼 보였습니다. 하나의 Layer를 두개로 늘려줬을 뿐인데 그동안 풀리지 않았던, 케케묵은 과제 중 하나였던 XOR problem을 너무나도 간단하게 해결해 주었기 때문입니다. 그렇다면 Layer의 수를 증가시킬 수록 더 좋은 학습능력을 지니게 될 것이라고 생각하였습니다. 하지만 현실은 그렇게 간단치 못했습니다. 모든 것을 학습할 수 있을 것이라 생각되었던 딥러닝은 오히려 Layer의 개수가 많아지게 될 경우 각각의 뉴런들에서 제대로 된 학습이 이루어지지 않았습니다. 이러한 현상을 Vanishing gradient라고 합니다.
* Vanishing Gradient
Vanishing gradient의 문제는 꽤 많은 시간을 끌었지만 생각보다 간단하게 해결되었습니다. 학습의 과정에서 Gradient Descent Algorithm을 사용하며 우리는 미분을 계속 봐왔습니다. 미분은 일종의 영향력을 표현하는 논리입니다. 예를 들어, y에 대한 x의 영향력을 표현하기 위해 우리는 다음과 같이 미분을 사용합니다.
![]()
위와 같은 Nueral net이 있다고 생각해봅시다. 는 Input이고
는 output 입니다. 우리는
에 대한
의 영향력을 찾아내는 것이 학습입니다. 가설을 설정하고 cost function을 만드는 과정에서 우리는 여러 연산과 함수를 이용해왔습니다. 이 한계는 현재까지 우리가 Neural net에서 사용한 함수(Activationi function)를 상기시켜보면 해결할 수 있습니다. 특히 sigmoid 함수를 사용했는데 이 함수가 Vanishing gradient의 주요 원인이었다는 사실이 밝혀졌습니다.
그 이유는 sigmoid 함수의 값과 미분값이 0~1로 제한되어 있기 때문입니다. 1보다 작은 양수는 여러 단계의 곱셈 연산을 거치면 매우 작아집니다. 다시 말해 Layer의 개수가 많으면 많을수록, 학습 단계가 깊으면 깊을수록 영향력의 크기가 미미해져 학습이 제대로 되지 않는 것입니다. 1보다 작은 수를 계속 곱하게 되면 결국 최종값은 매우 작아질 수 밖에 없습니다.
다음 포스트에서 Vanishing gradient 현상을 어떤 함수를 통해 감쇄시킬 수 있는지 알아보도록 하겠습니다.