Scikit-learn의 Iris 데이터셋 분류하기
Iris Dataset 분류하기
Scikit-learn의 기본적인 dataset 중에 4가지 특성으로 아이리스 꽃을 분류하는 예제가 있습니다,
01. 데이터 로드
#-*- coding: cp949 -*- #-*- coding: utf-8 -*- import math import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import load_iris data = load_iris()
02. 데이터 구조 파악하기
data는 하나의 클래스 객체인데 dict의 형식을 따르고 있는 것처럼 보입니다. dict는 아닙니다…
print(data)
* 출력값
{‘data’: array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2], …), ‘target’: array([0, 0, 0, 0, 0, 0, 0, 0, … ]), ‘target_names’: array([‘setosa’, … ]), …
print(data.keys())
* 출력값
dict_keys([‘data’, ‘target’, ‘target_names’, ‘DESCR’, ‘feature_names’])
1) data에는 각 꽃의 특성(feature)이 담겨있습니다.
2) target은 data array와 짝이 일치합니다(어떤 식인지는 모르겠지만 이어져 있는 것 같습니다). 이는 각 행이 어떤 꽃을 나타내는지를 알려줍니다.
– 0: Setosa, 1: Versicolor, 2: Virginica <– target_names에 담겨있는 내용
3) feature_names에는 data의 특성이 무엇을 의미하는지 알려준다.
– [‘sepal length (cm)’, ‘sepal width (cm)’, ‘petal length (cm)’, ‘petal width (cm)’] * sepal: 꽃받침 / petal: 꽃잎
각각의 value를 이용하기 쉽게 하나의 변수에 담아옵니다.
features = data.data # shape = (150, 4) feature_names = data.feature_names target = data.target target_names = data.target_names
다음과 같이 그래프 상에 산점도로 나타낼 수 있습니다.
for t in range(3):
if t == 0:
c='r'
marker='>'
elif t == 1:
c='g'
marker='o'
elif t == 2:
c='b'
marker='x'
plt.scatter(features[target == t, 0], # sepal length
features[target == t, 1], # sepal width
marker = marker,
c = c)
plt.xlabel("sepal length")
plt.ylabel("sepal width")
* 저는 features[target == t, 0] 이라는 문장이 굉장히 낯설었습니다. 이 때문에 위에서 data와 target이 연결되어 있는 것 같다고 설명했는데 사실은 연결이라기 보다는 Numpy 배열의 특징이라고 봐야겠습니다. Numpy 배열에서는 bool 배열을 이용해서 슬라이싱이 가능합니다. 즉 다시 말해 target == 0 (Setosa) 은 [True, True, True, … False, False … ]의 배열이 됩니다. 그러므로 features[target == 0, 0]은 Setosa의 Feature 중 0번째, 즉 Sepal length 만 뽑아오겠다는 소리입니다. <fn>http://sinpong.tistory.com/120</fn>
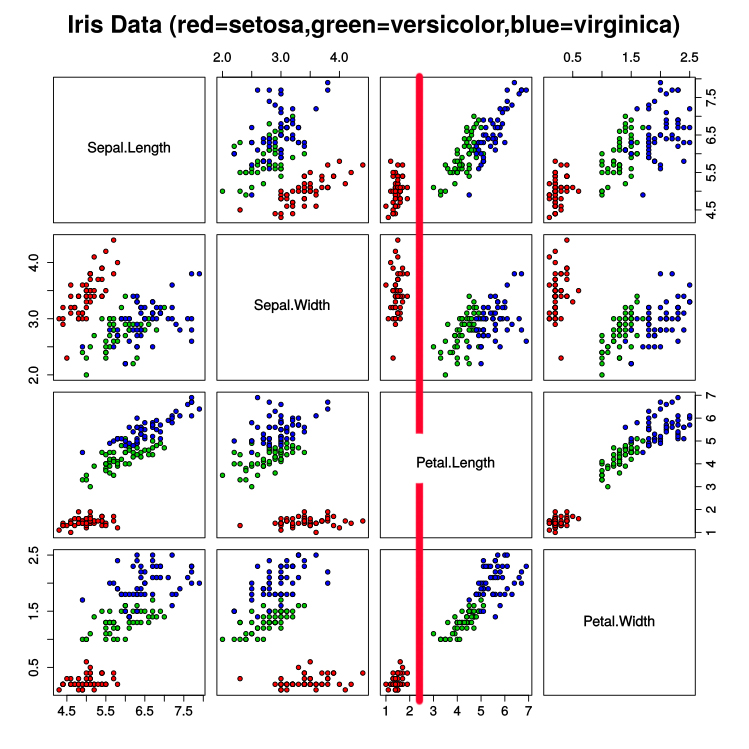
03 Setosa 분류하기
우리는 세 종류의 아이리스를 분류해야 합니다. 산점도를 잘 보면 빨간색(Setosa)는 Petal length만으로도 쉽게 분류할 수 있는 것을 할 수 있습니다. Setosa의 petal length 최댓값이 나머지 두 아이리스의 petal length 최솟값보다 작기 때문입니다.
petal length를 담은 배열을 가져옵시다.
plength = features[:, 2]
그 다음 Setosa의 petal length만을 가져오기 위한 작업을 해봅시다. 위에서 target은 0, 1, 2로 이루어진 원소 150개의 배열입니다. 우선, 이 정수형 배열을 문자열 배열(labels)로 바꿔줍니다.
labels = target_names[target]
이 문자열 배열을 가지고 Setosa만 True를 나타내는 불 배열을 만들어 줍니다.
is_setosa = (labels == 'setosa')
Setosa’s petal length의 최댓값과 Non-Setosa’s petal length의 최솟값을 비교해봅시다.
max_setosa =plength[is_setosa].max()
min_non_setosa = plength[~is_setosa].min()
print('Maximum of setosa: {0}.'.format(max_setosa)) # 1.9
print('Minimum of others: {0}.'.format(min_non_setosa)) # 3.0
이로써 우리는 Setosa의 경우 단순하게 petal length 만으로 구분할 수 있다는 것을 알게 되었습니다. 물론 이는 기계학습은 아닙니다. 이 구별점을 자동으로 찾도록 코드를 작성하는 것이 기계학습입니다.
04 Versicolor와 Virginica 분류하기
나머지 두 아이리스 종을 분류하는 것도 위와 같은 방법을 이용해보려 합니다. 다만 Setosa를 분류해낼 때 처럼 100% 분류하는 기준은 없을 것입니다. 최대한 오류를 줄일 수 있는 기준을 찾는 코드를 작성해보도록 합시다.
Setosa 분류는 끝났으니 범주를 좁히도록 합시다.
features = features[~is_setosa] labels = labels[~is_setosa]
Versicolor로부터 Virginica를 분류해내기 위해 Virginica를 나타내는 불 변수를 만듭니다.
is_virginica = (labels == 'virginica')
이제 정확도(acc)를 가장 높이는 모델을 만들어낼 것입니다. 그렇다면 우리는 4가지 속성 각각에 대해 값을 조금씩 조정해가며 예상값과 실제값이 같은 비율이 많아지는, 다시 말해 정확도가 가장 높은 ‘기준’과 ‘그 기준의 경계값’을 찾아낼 것입니다. (위에서 Setosa를 분류해내긴 기준은 petal length였고 기준은 1.9~3.0 사이의 수치가 되겠죠?)
먼저 가장 높은 정확도를 담을 변수를 하나 설정합시다. 새로운 정확도와 이를 비교해서 새로운 정확도가 더 높을 시 새로운 정확도로 대체하기 위함입니다.
best_acc = 0.0 # 일단 0%로 설정해놓습니다.
모든 속성에 대하여, 모든 속성의 값을 보기위해 for 구문을 두번 사용합니다.
# feature에는 0, 1, 2, 3이 담깁니다.
for feature in range(features.shape[1]):
# feature는 각각 septal length, septal width, petal length, petal width를 나타냅니다.
threshold = features[:,feature]
for t in threshold:
# 경계값 t와 비교하기 위해 실제값을 가져옵시다.
# 사실 경계값 t는 실제값 중 하나로 지정됩니다.
feature_i = features[:, feature]
# t보다 큰 feature_i를 모두 True라고 지정합니다.
# 다시 말해 모두 Virginica라고 예상을 합니다.
pred = (feature_i > t)
# Virginica라고 예상한 것이 얼마나 실제(is_virginica)와 맞는지 비교합니다.
# 맞으면 1, 틀리면 0으로 나올테니 평균(mean)을 내줍니다.
acc = (pred == is_virginica).mean()
# 오히려 반대의 경우가 정확도가 더 높을 수도 있습니다.
rev_acc = (pred == ~is_virginica).mean()
# 그럴 경우 두 값을 바꿔줍니다.
if rev_acc > acc:
reverse = True
acc = rev_acc
else:
reverse = False
# 만약 새로운 acc가 여태까지의 best_acc보다 높았다면 새로운 acc가 best_acc가 됩니다.
if acc > best_acc:
best_acc = acc
best_fi = fi
best_t = t
best_reverse = reverse
print(best_fi, best_t, best_reverse, best_acc)
* 출력값
best_fi: 3, best_t = 1.6, best_reverse = False, best_acc = 0.94
features[3], 즉 petal width를 기준으로 경계값을 1.6으로 했을 때 그보다 큰 것을 Virginica, 작은 것을 Versicolor라고 하면 약 94%의 정확도로 분류를 해낼 수 있다는 뜻이네요.
05. 교차 검증
위에서 우리는 모든 데이터를 가지고 훈련을 하였고 같은 데이터로 정확도를 테스트하였습니다. 우리는 새로운 데이터에 대해 모델이 얼마나 잘 작동하는 지를 평가해야 합니다. 하지만 모든 데이터를 가지고 훈련을 하게 되면 Overfitting의 문제가 발생합니다. 이를 막기 위한 것이 교차 검증입니다. 전체 데이터 중 일부만을 훈련에 사용하고 나머지는 검증에 사용하자는 것입니다.
전체 데이터를 두 부분으로 나누어 하나는 훈련용, 하나는 검증(Validation)용으로 사용합니다. 예를 들어 100개의 데이터가 있다면 70개를 학습용, 30개를 검증용으로 지정합니다. 70개로 우선 모델을 만들고 나머지 30개로 모델이 잘 만들어졌는지를 평가하게 됩니다. 꼭 30개를 검증용으로 나두어야 하는 것은 아닙니다. 절반을 검증용으로 남겨둘 수도 있고 심지어 1개만을 검증용 데이터로 빼놓을 수도 있습니다. 그 방법 역시 여러가지입니다.
01) The Validation set Approach
전체 데이터 중 학습용과 검증용을 각각 50% 씩 지정하여 모델을 학습시키는 방법입니다. 가장 큰 단점은 꽤 적은 데이터만을 학습용으로 사용한다는 것입니다. 절반씩 나눈 데이터가 서로 특성이 매우 다르다면 곤란하겠지요. 편향될 수 있다(High bias)는 것이 최대 단점입니다.
02) Leave one out cross Validation(LOOCV)
단일 잔류 검증입니다. 오직 단 하나의 데이터 포인트만을 검증용으로 빼두는 것입니다. 단, 이 과정을 모든 데이터 포인트마다 하는 것입니다. 즉 n개의 데이터가 있다면 1개를 검증용으로, 나머지 (n-1)개를 학습용으로 하되 이러한 과정을 n번 거치는 것입니다. 문제점은 시간이 많이 걸린다는 것입니다. 1번 방법이 1번의 학습, 1번의 검증으로 이루어져 있었다면 LOOCV는 n번의 학습, n번의 검증이 필요합니다.
03) k-fold cross validation
가장 합리적인 방법은 1번과 2번 방법을 혼합하는 것입니다. 큰 골격은 LOOCV를 따라갑니다. 1개의 데이터 포인트만을 검증용으로 남겼던 방법과는 달리 10%, 혹은 20%의 데이터를 검증용으로 사용합니다. 그 후 LOOCV처럼 검증용 데이터를 바꿔가며 과정을 반복합니다. 검증용 데이터가 10%였다면 총 10번, 20%였다면 총 5번 과정을 반복합니다.