[DSP 01] 이산시간 신호와 시스템의 시간영역 해석

DT = Discrete time
CT = Continuous time

1. DT 신호의 표현

1) 샘플링으로 얻어진 DT 신호의 표현

샘플링을 \( T_s \)초마다 하는 경우

\( x[n] = x(t) | _{t=nT_s} = x(nT_s) \)

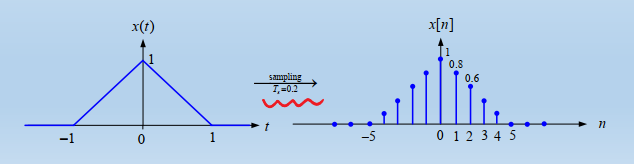
DT 신호의 표현 방법

함수로 표현 \( x[n] = 2cos(\frac{n}{5}+\frac{\pi}{4}) \)

Sequence로 표현 \( x[n] = \lbrace \frac12, \frac34, 1, 0, -1, \frac13 \rbrace \)
– 수열 집합 외의 신호 샘플은 0으로 본다.
– 화살표: \( n=0 \) 의 위치 (화살표가 없으면 첫번째가 \( n = 0 \))
– causal signal (\( x[n] = 0 for n<0 \))

신호의 유형

Continuous	주기	Fourier Series
	비주기	Fourier Transform
Discrete	주기	DT Fourier Series
	비주기	DT Fourier Transform

CT 주기 신호를 샘플링하면 주기 또는 비주기 신호 DT 신호가 된다.
– sampling interval에 따라 주기 or 비주기 여부가 달라진다.

DT 정현파 신호가 Sampling 이후 주기적이기 위한 조건

\( x[n] = Asin(2\pi f_0n), ~ x[n+N] = Asin(2\pi f_0n+2\pi f_0 N) \)

\( m = 2\pi f_0 N \) 일 때 정규화 주파수 \( F = \frac mN \) 가 유리수일 때 주기적 신호가 된다.

---

주기가 \( T \) 인 \( CT \)주기 신호를 \( T_s \) 간격으로 샘플링한 경우

\( mT = NT_s \rightarrow \frac{T}{T_s} = \frac Nm (N, m: integer) \)

---

여기서 \( T \)는 시간을 가리킨다. \( F \)를 주파수라고 한다면

\( T = \frac 1F \)

---

2. 기본 DT 신호

1) Unit Step Function

\( u[n] = \begin{cases} 1&~~~n \ge 0 \\ 0 & ~~~ n < 0 \end{cases} \)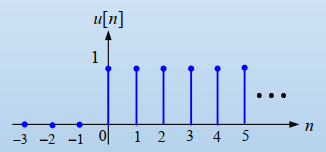

2) Unit Ramp Function

\( u[n]=\begin{cases} 1 & n\ge 0 \\ 0 & n<0 \end{cases} \)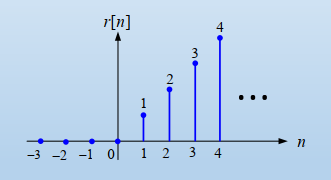

3) Unit Pulse Function

\( \delta [n] = \begin{cases} 1 & n=0 \\ 0 & n \neq 0 \end{cases} \)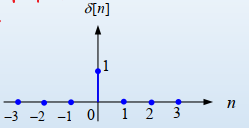

DT pulse function의 성질

1. \( u[n] – u[n-1] = \delta[n] \)
2. \( \sum_{k = -\infty}^{n} \delta[k] = u[n] \)
3. sampling 성질: \( x[n] \delta[n-n_0] = x[n_0]\delta[n-n_0] \)
4. sifting 성질: \( \sum\nolimits_{n=-\infty}^{\infty} x[n] \delta[n-n_0] = x[n_0] \) — \( n=n_0 \) 일때만 값이 있으므로
5. convolution 성질 \( \sum_{k=-\infty}^{\infty} x[k] \delta[n-k] = x[n] *\delta[n] = x[n] \) — \( k=n \) 일 때만 값이 있으므로 어떤 \( x \)에 \( \delta \)을 convolution 하면 \( x \) 자체가 나온다.

cf. CT impulse function

1. \( du(t) / dt = \delta (t) \)
2. \( \textstyle \int_{-\infty}^t \delta(\lambda)d\lambda = u(t) \)
3. \( \textstyle \int_{-\infty}^{\infty} \delta(t) f(t) dt = f(0) \)
4. \( \textstyle \int_{-infty}^{\infty} f(t-t_0) f(t)dt = f(t_0) \)