활용

이번 Logistic Classification 학습에서는 이론에 앞서 활용방안부터 살펴보겠습니다. Logistic Classification은 binary하게 분류하는 것을 말합니다. 즉 True / False 와 같이 이분법적으로 데이터를 분류하는 것을 의미합니다. 예를 들어 어떠한 메일이 도착하였을 때 이 메일을 정상 메일(Ham)로 분류할지 스팸 메일(Spam)로 분류할지 결정하는 것이 바로 Logistic Classification 입니다. 다른 예시로는 페이스북 사용자의 ‘좋아요’ 정보를 입력받아 분석하여 사용자의 뉴스피드에 어떠한 게시물을 보여줄지 말지를 결정하는 것도 있겠습니다. 또한 신용카드 과거 거래 내역을 분석하여 패턴을 익힌 후 신용카드를 사용하였을 때 이번 사용이 과연 원래 주인이 사용한 것인지 판단하는 데에도 해당 원리가 들어갑니다.
의학에 접목 시켜보면 몸 속에서 종양(덩이)를 발견했을 때 그 종양이 양성인지 악성인지 판단하는 것 역시 Logistic Classification 을 활용한 예입니다.

이론

Linear Regression을 벗어나 이번엔 Logistic classification에 대해 배워보도록 하겠습니다. 어찌보면 이전보다 더 단순하지만 실상은 더 복잡한 녀석이라는 생각이 듭니다. 큰 이론은 변하지 않습니다. 역시나 H(ypothesis)C(ost)G(radient descent)의 논리를 따라갑니다.

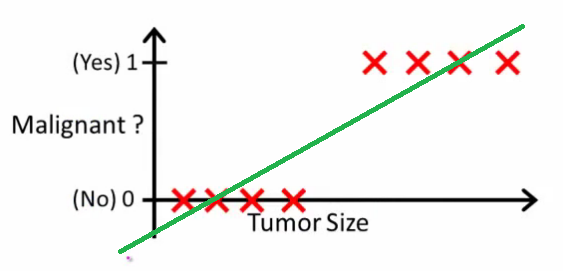
위 그림에서는 단순하게 종양의 크기만을 가지고 양성(0), 악성(1)을 나누고 있습니다. 크기가 크면 악성 종양, 크기가 작으면 양성 종양으로 판단을 하고 있고 초기 데이터로 각각 4개씩 주어졌습니다. 양성과 악성을 나누는 Tumor Size의 y값이 대략 0.5 쯤 되는군요. 다시 말해 1차원 함수 상 y의 값이 0.5보다 크면 악성, 0,5보다 작으면 음성으로 판단할 수 있습니다.  지금의 경우에는 완벽하게 양성과 악성이 구분됩니다.

문제는 새로운 데이터가 삽입될 때 발생합니다. 만약 현재 그래프 상에 표시된 종양들보다 크기가 훨씬 더 큰 악성 종양이 학습 데이터로 주어졌다고 해봅시다. 그 경우 초록색 그래프의 기울기는 작아지게 됩니다. 크기가 아주 큰 악성 종양을 학습하면 학습할 수록 그래프는 점점 내려갈 것입니다. 그렇게 자꾸 내려가면 y의 값이 0.5가 되는 Tumor Size가 자꾸 커지게 됩니다. 그러다가는 결국 초기 데이터 상에서 주어졌던 “가장 작은 악성 종양”을 양성으로 판단하게 되는 날이 오게 되겠죠.

01) Hypothesis

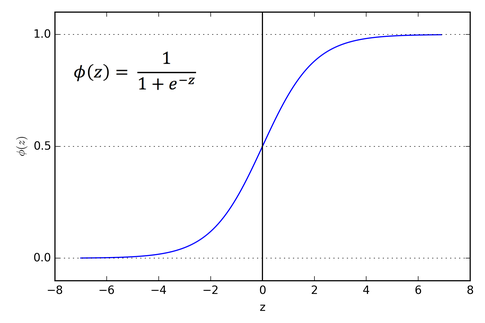
위의 설명을 통해 우리는 가설을 단순하게 이전처럼  로 표현하면 안된다는 것을 깨달았습니다. 이를 대체하기 위해서는 우선 ① y가 0~1 사이의 값만을 가지면 좋겠고 ② 구분점에서 그래프 모양이 급격하게 변하면 좋겠습니다. 그래서 우리는 아래와 같은 새로운 함수를 가설로 설정합니다.

왜냐하면 이 함수의 그래프 모양이 이렇게 생겼거든요.

02) Cost function

이번 역시 cost를 최대한 감소시키는 것이 관건입니다. 기본적으로 cost는  , 즉 측정값과 실제값의 차이입니다. 이렇게 쓸 경우 전체를 다 더하는 것의 의미가 없어지기 때문에(양수 음수…) 우리는 차의 제곱의 합의 최솟값을 구하고자 한 것입니다.

이전처럼  를 할 경우 하나의 문제점이 발생합니다. 동일하게 Gradient Descent Algorithm을 사용하게 될텐데 이전과 마찬가지로 cost function을 설정한다면 학습이 제대로 이루질 수가 없습니다. Gradient Descent Algorithm의 핵심은 Convex한 그래프를 따라 점이 점차 이동하여 일종의 극소점에 도달하게 하는 것입니다. <fn>http://kmkidea.tistory.com/15</fn>

   

Linear Regression의 cost가 왼쪽 모양이었다면 이번 단원의 cost는 오른쪽 모양을 가집니다. 극소점이 굉장히 많죠? 이 상태에서 학습을 실행할 경우 곳곳에 숨어있는 극소점들(local minimum)을 마치 최소점(global minimum)인 것으로 착각하여 학습의 오류를 가져옵니다.

따라서 우리는 다른 cost 함수를 찾아야 하고, 다음과 같은 함수를 만들었습니다.

는  와 거의 흡사하게 움직이기 때문에 각각의 함수들 역시  와 모양이 비슷할 것입니다. <fn>http://desmos.com</fn>

먼저  일 때의 그래프  입니다.  이므로 우리가 볼 그래프는 제 1사분면에만 존재합니다.  일 때  역시 1이라면 이 둘의 차이인 cost는 0이 됩니다. 즉, “cost 최소화하기” 과정을 통해 그래프 상에서 내려가는 학습을 진행할 수 있습니다.

 

반대의 경우 역시 마찬가지입니다.  일 때  역시 0이라면 cost는 0이 됩니다. 마찬가지로 “cost 최소화하기” 과정을 통해 그래프 상에서 내려가는 알고리즘을 써먹을 수 있게 된 것입니다.

를 하나의 식으로 표현하면  가됩니다.

따라서   가 되고 이를 풀어쓰면 최종적으로

가 됩니다.

03) Gradient Descent Algorithm

이제는 이 알고리즘을 쓸 수 있게 되었습니다.

 

실습

코딩의 상황은 이러합니다. 학생 6명의 이론 공부 시간과 실습 시간을 X의 초기 데이터로 전달합니다. 아래 코드에서 첫번째 학생은 1시간 동안 이론 공부를 하였고 3시간 동안 실습을 하였네요. Y는 시험의 통과 유무를 나타냅니다. 방금 그 학생은 안타깝게(?) 시험에 통과하지 못하였습니다.

import tensorflow as tf

x_data = [[1, 3], [2, 1], [3, 0], [4, 2], [5, 5], [2, 6]]
y_data = [[0], [0], [0], [1], [1], [1]]

X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

# 변수 및 가설 설정
W = tf.Variable(tf.random_normal([2, 1]), name = "weight")
b = tf.Variable(tf.random_normal([1]), name = "bias")

hypothesis = tf.sigmoid(tf.matmul(X, W) + b)

# cost function
cost = -tf.reduce_mean(Y * tf.log(hypothesis)+(1-Y)*tf.log(1-hypothesis))

# Gradient Descent Algorithm
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)

# cast 함수로 hypothesis > 0.5 명제를 float32로 변환
# hypothesis가 0.5보다 크다면 1.을 0.5보다 작거나 같으면 0.을 return
predicted = tf.cast(hypothesis > 0.5, tf.float32)

# equal 함수로 예상값(predicted)과 실제값(Y)이 같은지 비교 후
# True/False 결과를 float32로 cast시키고
# 시행 전체의 평균을 reduce_mean으로 구함
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), tf.float32))

# session
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for step in range(2001):
        # 일단 결과 출력 없이 훈련만 시켜보았습니다.
        sess.run([train], feed_dict={X:x_data, Y:y_data})

    # 그 후 테스트를 해보았습니다.
    # 이 코드는 반드시 세션 상에서 실행되어야 합니다.
    p_val, h_val =sess.run([predicted, hypothesis], feed_dict={X:[[1, 5], [10, 5], [4,5]]})
    print(p_val)
    print(h_val)

결과는

[[ 1.]
[ 1.]
[ 1.]]
[[ 0.76879722]
[ 0.96437287]
[ 0.86994559]]

입니다.

첫번째 학생은 이론 공부 시간이 많이 부족했는데도 불구하고 실습 시간이 많아 시험에 합격했네요.

 

# Lab 5 Logistic Regression Classifier
import tensorflow as tf
tf.set_random_seed(777)  # for reproducibility

x_data = [[1, 2],
          [2, 3],
          [3, 1],
          [4, 3],
          [5, 3],
          [6, 2]]
y_data = [[0],
          [0],
          [0],
          [1],
          [1],
          [1]]

# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([2, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

# Hypothesis using sigmoid: tf.div(1., 1. + tf.exp(tf.matmul(X, W)))
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)

# cost/loss function
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) *
                       tf.log(1 - hypothesis))

train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)

# Accuracy computation
# True if hypothesis>0.5 else False
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())

    for step in range(10001):
        cost_val, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
        if step % 200 == 0:
            print(step, cost_val)

    # Accuracy report
    h, c, a = sess.run([hypothesis, predicted, accuracy],
                       feed_dict={X: x_data, Y: y_data})
    print("\nHypothesis: ", h, "\nCorrect (Y): ", c, "\nAccuracy: ", a)